From Complexity to Clarity: Simplifying Principal Component Analysis (PCA)
"Principal Component Analysis (PCA) is by far the most popular dimensionality reduction algorithm. It is a statistical procedure which is also used for finding patterns in high dimension data. It uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called as principal components."
Principal Component Analysis: Because Your Data Has Too Many Opinions, Just Like Your Ex Used To 🤭
1.) What even is PCA?
2.) Why PCA? or, "Why Shrink Your Data?"
3.) How does PCA actually works?
4.) Application of PCA (Yes people actually use it)
5.) Math Stuff
6.) Python Coding Example
7.) Conclusion: Do you really need it?
1. What Even Is PCA?
* Definition: Principal Component Analysis — or, as we like to call it, "Magic Math that Makes Your Data Less Annoying."* Simple Explanation: It’s where we take a perfectly fine dataset, perform a mathy shuffle dance, and end up with fewer columns that apparently contain the same enough information. Simple, right?
* Behind the Scenes: Eigenvalues, eigenvectors, matrices… you know, all the good stuff you happily forgot after that one linear algebra class.
2. Why PCA? Or, "Why Shrink Your Data?"
* To Stop Crashing Your Laptop: Imagine actually trying to work with a 100-dimensional dataset. PCA helps avoid the horror of infinite loading circles.* Because Interpretability Is for Amateurs: With PCA, you can have the thrill of knowing your data just got simpler without needing to explain why.
* Optimal Confusion Guarantee: Impress your friends and baffle your audience with reduced dimensions that convey almost the same story. Who doesn’t love a good riddle in data form?
3. How Does PCA Actually Work?
* Step-by-Step Guide: A 15-step process of complex calculations, conveniently glossed over in most blog posts. But don’t worry — you can just use a library function! I have covered that in 6 steps.* Scaling Your Data Like a Pro: Normalize first, or you’ll end up with results that don’t make sense (not that they ever really do).
* Covariance and Variance Fun: Rejoice in knowing how much variation you can squeeze out of your data without it screaming back in protest.
4. Applications of PCA (Yes, People Actually Use It)
* Dimensionality Reduction (Obviously): Because who needs all those columns when you can turn them into just a few "principal components"? Image Compression, a.k.a. “Why’s My Picture Blurry Now?” Ever wonder how to shrink images into an indecipherable mosaic? PCA’s got you covered.* Pattern Recognition and ML Models: You’ll get to say you improved your model’s performance by 0.02% and act like it’s groundbreaking.
* Noise Reduction (Or Data Disguising): PCA will kindly help you ignore all the pesky little outliers you didn't want to deal with.
5. Math Stuff
This section is for nerds, who are interested in the math behind this algorithm.Steps to perform PCA:
(i) Standardize the dataset.
(ii) Calculate the covariance matrix for the feature in data.
(iii) Calculate the eigen values and eigen vectors for covariance matrix.
(iv) Sort eigen values and their corresponding eigen vectors.
(v) Pick k eigen values and form a matrix of eigen vector.
(vi) Transform original matrix.
(i) Standardize the dataset.
Training Data Table
| Feature 1 | Feature 2 | Feature 3 | Feature 4 |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| 5 | 5 | 6 | 7 |
| 1 | 4 | 2 | 3 |
| 5 | 3 | 2 | 1 |
| 8 | 1 | 2 | 2 |
- z: The standardized value (z-score).
- x: The original data point.
- μ: The mean of the dataset.
- σ: The standard deviation of the dataset.
| Feature 1 | Feature 2 | Feature 3 | Feature 4 | |
|---|---|---|---|---|
| μ = | 4 | 3 | 3 | 3.4 |
| σ = | 3 | 1.58 | 1.73 | 2.30 |
| Feature 1 | Feature 2 | Feature 3 | Feature 4 |
|---|---|---|---|
| -1 | -0.63 | 0 | 0.26 |
| 0.33 | 1.26 | 1.73 | 1.56 |
| -1 | 0.63 | -0.57 | -0.17 |
| 0.33 | 0 | -0.57 | -1.06 |
| 1.33 | -1.26 | -0.57 | -0.60 |
(ii) Calculate the covariance matrix for the feature in data.
| Feature 1 | Feature 2 | Feature 3 | Feature 4 | |
|---|---|---|---|---|
| Feature 1 | var(f1) | cov(f1,f2) | cov(f1,f3) | cov(f1,f4) |
| Feature 2 | cov(f2,f1) | var(f2) | cov(f2,f3) | cov(f2,f4) |
| Feature 3 | cov(f3,f1) | cov(f3,f2) | var(f2) | cov(f3,f4) |
| Feature 4 | cov(f4,f1) | cov(f4,f2) | cov(f4,f3) | var(f4) |
| Feature 1 | Feature 2 | Feature 3 | Feature 4 | |
|---|---|---|---|---|
| Feature 1 | 0.8 | -0.25 | 0.03 | -0.14 |
| Feature 2 | -0.25 | 0.8 | 0.51 | 0.49 |
| Feature 3 | 0.03 | 0.51 | 0.8 | 0.75 |
| Feature 4 | -0.14 | 0.49 | 0.75 | 0.8 |
(iii) Calculate the eigen values and eigen vectors for covariance matrix.
| Feature 1 | Feature 2 | Feature 3 | Feature 4 | |
|---|---|---|---|---|
| Feature 1 | 0.8-λ | -0.25 | 0.03 | -0.14 |
| Feature 2 | -0.25 | 0.8-λ | 0.51 | 0.49 |
| Feature 3 | 0.03 | 0.51 | 0.8-λ | 0.75 |
| Feature 4 | -0.14 | 0.49 | 0.75 | 0.8-λ |
| 0.8-λ | -0.25 | 0.03 | -0.14 |
| -0.25 | 0.8-λ | 0.51 | 0.49 |
| 0.03 | 0.51 | 0.8-λ | 0.75 |
| -0.14 | 0.49 | 0.75 | 0.8-λ |
| v1 |
| v2 |
| v3 |
| v4 |
| e1 | e2 | e3 | e4 |
|---|---|---|---|
| 0.16 | -0.91 | -0.30 | 0.19 |
| -0.52 | 0.20 | -0.81 | 0.12 |
| -0.58 | -0.32 | 0.18 | -0.72 |
| -0.59 | -0.11 | 0.44 | 0.65 |
| e1 | e2 |
|---|---|
| 0.16 | -0.91 |
| -0.52 | 0.20 |
| -0.58 | -0.32 |
| -0.59 | -0.11 |
| Feature 1 | Feature 2 | Feature 3 | Feature 4 |
|---|---|---|---|
| -1.00 | -0.63 | 0.00 | 0.26 |
| 0.33 | 1.26 | 1.73 | 1.56 |
| -1.00 | 0.63 | -0.57 | -0.17 |
| 0.33 | 0.00 | -0.57 | -1.04 |
| 1.33 | -1.26 | -0.57 | -0.60 |
| e1 | e2 |
|---|---|
| 0.16 | -0.91 |
| -0.52 | 0.20 |
| -0.58 | -0.32 |
| -0.59 | -0.11 |
| nf1 | nf2 |
|---|---|
| 0.01 | 0.75 |
| -2.55 | -0.78 |
| -0.05 | 1.25 |
| 1.01 | 0.00 |
| 1.57 | -1.22 |
6. Python Coding Example
# Code Example: import pandas as pd import numpy as np # Input data A = np.matrix([[1, 2, 3, 4], [5, 5, 6, 7], [1, 4, 2, 3], [5, 3, 2, 1], [8, 1, 2, 2]]) # Create DataFrame df = pd.DataFrame(A, columns=["f1", "f2", "f3", "f4"]) # Standardize the data df_std = (df - df.mean()) / df.std() # Number of Principal Components n_components = 2 # Apply PCA from sklearn.decomposition import PCA pca = PCA(n_components=n_components) pc = pca.fit_transform(df_std) # Convert PCA results to DataFrame principalDf = pd.DataFrame(data=pc, columns=["nf" + str(i + 1) for i in range(n_components)]) # Display output print(principalDf)
Output
| Index | nf1 | nf2 |
|---|---|---|
| 0 | -0.014003 | -0.755975 |
| 1 | 2.556534 | 0.780432 |
| 2 | 0.051480 | -1.253135 |
| 3 | -1.014150 | -0.000239 |
| 4 | -1.579861 | 1.228917 |
Probably not, but it sure sounds fancy when you tell people at parties, right? If you love mysterious statistical transformations, you’re going to adore PCA!
I hope this helped you. If it did then please share it with your friends and spread this knowledge.
Follow us at :
Instagram :
https://www.instagram.com/infinitycode_x/
Facebook :
https://www.facebook.com/InfinitycodeX/
Twitter :
https://twitter.com/InfinityCodeX1




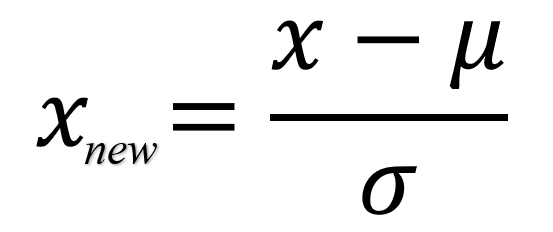


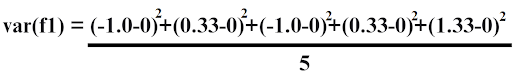





No comments:
No Spamming and No Offensive Language