K-Means Clustering
Clustering is a type of Unsupervised Learning where
you find patterns & data that you are working on; it may be the shape,
size, color, etc… Which can be used to
group data items or create clusters. This method is commonly used on the dataset
of small size to model & analyze the data.
Basically, there are 3 types of Clustering :
(i) Exclusive Clustering
(ii) Overlapping Clustering
(iii) Hierarchical Clustering
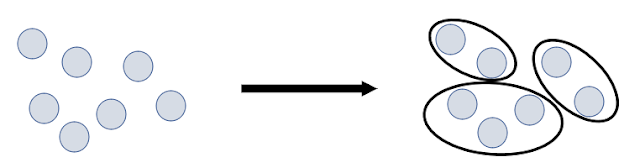
(i) Exclusive Clustering :
This Exclusive Clustering is a Hard clustering
in which the data points or the items exclusively belong to one cluster. An example of this kind of clustering is K-Means Clustering.
Both of these clusters are completely different and
not at all related to each other.
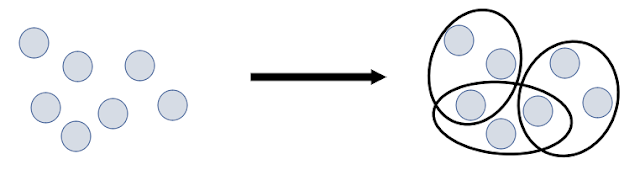
(ii) Overlapping Clustering :
This Overlapping Clustering is a Soft clustering
in which the data points or the items exclusively belong to multiple clusters. An example of this kind of clustering is Fuzzy, C-Means Clustering.
As you can see that the some of the blue data points
are overlapping the red data points.
(iii)Hierarchical Clustering :
When 2 clusters have a parent-child relationship
or a tree-like structure then it is a Hierarchical Clustering.
In Hierarchical Clustering, there are 2 types of
approach :
(a) Agglomerative :
Which supports the Bottom-Up approach. We begin with the
whole set and proceed to divide it into successively smaller clusters.
(b) Divisive :
Divisive Clustering is a Top-Down approach it, we begin
with the whole set and proceed to divide it into successively smaller clusters,
Out of several types of clustering today our main focus
will be on K-Means Clustering.
Our Agenda for this Blog post :
1.) What is K-Means Clustering?
2.) How does K-Means Clustering work?
3.) Application of K-Means Clustering
4.) Advantages and Disadvantages of K-Means Clustering
5.) K-Means Clustering Example
1.)What is K-Means Clustering?
K-Means Clustering is an Unsupervised Learning algorithm, unlike Supervised Learning in this case we don’t have any labeled
data. The number of groups or clusters is represented by “K”. The
algorithms then run iteratively assign each data points to one of the “K”
troops based on the features which are already provided.
2.)How does K-Means Clustering Works?
Let’s say we have a data set like this where X & Y
axis represents 2 different features and we want to identify clusters in this
data set. Now when the data set is given to us; we don’t have any information
on the target variable so actually we don’t know what we are looking for all we
are trying to do is identify some structure into this data set.
One way of looking into this is these 2 clusters i.e
C1 and C2 just by visual examination we can say that this data set has these 2
clusters and K-Means help us to identify these clusters. Now as I mentioned earlier
that “K” in K-Means clustering is a free parameter whenever we start the algorithm
we have to describe the value of “K” prior we jump into the algorithm. As you can
see in the image here the value of our “K” is 2.
Now there are 6 essential steps in K-Means :
(a) Identify the points :
The very first step is to identify the “K” random
points which we consider as the center of the clusters.
NOTE: Number of “K”
should be equal to the number of clusters. Each cluster should have only one
point.
Start with “K” centroid by putting them at a random
place on the 2D plane here K = 2. So the number of random points generated is
2.
(Start
with K centroids by putting them at a random place, Here K = 2)
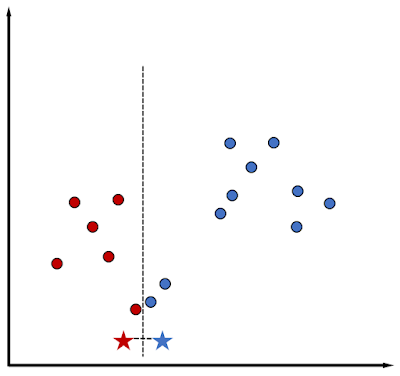
(b) Identify the Distance :
The second step in this is to identify the distance of
each data points from the centroids.
Now if we see the diagram below if some point is closer
to the Centroid 1 which is our Red Star then we can say that point belongs to Red
cluster and if some point is closer to the Centroid 2 which is our Blue-star then
we can say that point belongs to the Blue cluster. Now the simple way of identifying
the distance is to draw 2 lines where one line is horizontal between Red and
Blue centroid, whereas the second line will be perpendicular to that
horizontal line and the important thing here is to draw that perpendicular
vertical line exactly at the center of both the centroids.
Now as we divided both the sides which helped us to produce
2 clusters that are the first Red cluster and the second Blue clusters. Now congratulation
we got 2 imperfect clunky clusters. Now we will start to improve these clusters,
we will make them better and better at every stage. The way we will do that is first
we will try to adjust the centroid that is our red and blue stars form which we
had created 2 clusters. What I mean is that let’s currently focused at the red
cluster, look at all the points which are present in the red cluster, now let’s
try to find the center of gravity of that cluster and now what we are going to
do is that we are going to put our centroid 1 which is our Red star at the center
of that data points which belongs to the red cluster and we will be doing same
to the Blue cluster and centroid 2 which is our Blue star.
(Compute the distance of every point from centroid and cluster them accordingly)
(c) Adjust the Centroids :
So basically we will get this when we make the
adjustment. Now we will repeat the same process again. What I mean is that
again we will recompute the distance of each of these points from these centroids which are Red star and Blue star. If the points are nearer to the Red
star (centroid 1) then it belongs to the Red cluster and if the points are
closer to the Blue star (centroid 2) then it belongs to the Red cluster.
(Adjust
centroids so that they become center of gravity for the given cluster)
(d) Re-Cluster every point :
Then what we will do is that we will repeat the above
step once again i.e we will draw again an horizontal line and a vertical perpendicular
line at the center of that horizontal line.
Now if you have noticed that the points which were
once belong to the Blue cluster now belongs to the Red cluster because actually
they are now more near to the Red star which is our red centroid.
(Again
re-cluster every point based on their distance with centroid)
(e) Adjust Again :
Now we will keep on repeating this process you just
recalculate our centroids then recalculate the distance of individual data
points from these centroids and readjust the clusters until the point that none
of the data points change the cluster.
(Again
Adjust centroids)
(f) Recompute cluster :
Now if you see the above image there is only one point
i.e point Pn which is changing its cluster. Which was in blue cluster now it
is in Red cluster now and if you notice that after this we can't do any more
adjustments to our data set.
Hence we can say that this is our final clusters.
(Recompute
clusters and repeat this till data points stop changing clusters)
So here are the 6 steps for the K-Means.
Now the most important point here is that we need to
supply “K” to our algorithm. Now I know that you had this question that what is
the optimal value of “K”? because here we have 2-dimensional space in reality
we will be having so many features and it is not easy or I’ll rather say it difficult to visualize that data on a scatter plot so which “K” should we start
with?
So you wait for this answer is over guys. Actually
there is a technique which we called as elbow method which will help us
to find the optimal value of “K”.
Q.)What is Elbow Method and how to implement it?
Before diving directly into the Elbow method. Let’s say we
took our data to set a scatter plot and showed this to different individuals and ask
them how many clusters do they see in this scatter plot?
Some might say I see 4 clusters in this scatter plot.
Some individuals might say there are 6 clusters in this
scatter plot.
Now if you noticed that different individuals have different
opinions. So our job is to find out the optimal value of “K” for our scatter
plot here our Elbow method comes to rescue us.
NOTE: In K-Means If
we are Minimizing the distance between points in a cluster we are automatically
Maximizing the distance between the cluster.
Now what we do here is we initially take any random
value of “K” like saying we took K = 2 and we will try to compute Sum Of Square
Error. What it means is for each of the clusters we try to compute the distance of individual data points from the centroid we square it then we sum
it up.
So for the red cluster, we got the Sum Of Square Error
1 (SSE1). Now similarly for the second cluster, we will get the Sum Of
Square Error 2 (SSE2) and we actually do this for all our clusters, in
the end we will get the total sum of square error.
SSE
= SSE1 + SSE2 + SSE3 + … + SSEk
Actually, this step is essential because it helps us to
remove the negative values which help us to do the calculation in an easy way.
Now we had computed value of SSE for K = 2, so we
repeat the same process for K = n (n: number you want).
Once we have that number we draw a plot.
In this graph at the X-Axis, we had taken the value of “K”
from 1 to 10 and on the Y-Axis. Now here we will joint all the points.
If you see that as we increase the number of clusters
it will decrease the error now it’s kind of intuitive so think about it, at
some point we can consider all our data points as one cluster individual where
our SSE almost becomes zero.
Now the important thing here is to find out the elbow.
Now the elbow in this graph is at number 3. So the
points which suddenly change the shape of the graph’s curve is actually our perfect
value of “K”.
Now here is little code for that :
K_range = range(1,10)
SSE = [] # SSE K=1,2,3,... will be saved here
for K in K_range:
km = KMeans(n_clusters=K)
km.fit(df[['Age','Income']]) #What is our SSE? How we get it?
SSE.append(km.insertia_)
SSE
SSE = [] # SSE K=1,2,3,... will be saved here
for K in K_range:
km = KMeans(n_clusters=K)
km.fit(df[['Age','Income']]) #What is our SSE? How we get it?
SSE.append(km.insertia_)
SSE
#Plot into chart
plt.xlabel('K')
plt.ylabel('SSE')
plt.plot(K_range,SSE)
plt.ylabel('SSE')
plt.plot(K_range,SSE)
Output :
Don't worry if you didn't get anything in this code I had explained it below in practical.
3.) Application of K-Means Clustering
K-Means clustering is used in varieties of examples such as
(i) Marketing
(ii) Biology
(iii) Entertainment
(iv) Academic Performance
(v) Search Engine
(i) Marketing :
Amazon is using popular it’s product recommendation system. For example Let’s say you want to purchase sports shoes and when you type sports shoes in the search bar of Amazon you will see all kinds of sport’s shoes of different brands and different features. This is where clustering comes it shows you the cluster of products that you want.
(ii) Biology :
Biologist uses various features to separate various type of creates into mammals, vertebrates, plants, etc. In which the mammals are the creatures which do not lay eggs and give birth to the child directly, where are the vertebrates are the species which lays eggs.
(iii) Entertainment :
The best example of the entertainment industry is Netflix it recommends the movies based on your previous watch history.
(iv) Acadmic Performance :
Based on the scores of the exam students are categorized in different categories such as A, B, C, D.
(v) Search Engine :
Clustering forms the backbone for search engines. When a search is performed the search results need to be grouped together as the user requirement.
4.) Advantages and Disadvantages of K-Means Clustering :
5.) K-Means Clustering Example :
So the problem we are going to solve is that we have a
data set in which we have the age and income of different people. Now clustering this
data points into various groups that we are going to find out is some
characteristics of these groups. Maybe the group belongs to the particular
group in America where the salaries are higher or the salaries are lower or
that group belongs to a certain profession where the salaries are higher versus
less.
So here is our Dataset :
# Import all the essential libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# Import our data set
data = pd.read_csv("D:\MY_ML\income.csv")
data.head()
data.head()
Output :
# extracting information from a dataset
data.info()
Output :
# Describing the dataset
data.describe().transpose()
Output :
# Plotting scatter plot
plt.scatter(data['Age'],data['Income'])
Output :
As we plot the scatter plot we can easily see the 3 clusters which are present in the diagram.
Creating a model where we will be using SKlearn library.
# Create Model
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3) #Number of Clustering is 3
km
km = KMeans(n_clusters=3) #Number of Clustering is 3
km
Output :
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
Run K-Means Algorithm on Age and Income, the Computed cluster as per our criteria where we told our algorithm to identify 3 clusters
#cluster 1 = 0
#cluster 2 = 1
#cluster 3 = 2
#cluster 2 = 1
#cluster 3 = 2
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3) #Number of Clustering is 3
km
km = KMeans(n_clusters=3) #Number of Clustering is 3
km
Output :
array([0, 0, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 2])
# Appending a new column
data['Cluster'] = y_pred
data.head()
data.head()
Output :
# Separating those 3 clusters into different dataframe
df1 = data[data.Cluster == 0]
df2 = data[data.Cluster == 1]
df3 = data[data.Cluster == 2]
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.xlabel('Age')
plt.ylabel('Income')
df2 = data[data.Cluster == 1]
df3 = data[data.Cluster == 2]
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.xlabel('Age')
plt.ylabel('Income')
Output :
As we can clearly see that our scatter plot has a little problem with it, So the Green cluster looks perfectly fine but the Red and Blue doesn't look fine. This problem occurs because our scaling is not correct our Y-Axis is scaled from 40000 till 160000 and the range of X-Axis is very narrow its like hardly 20 and on Y-Axis is 120000. So when we don't scale our features properly we can face this kind of problem. That's why we have to do some preprocessing and use MinMaxScaler which will help us to normalize our features.
# Using MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(data[['Income']])
data['Income'] = scaler.transform(data[['Income']])
scaler.fit(data[['Age']])
data['Age'] = scaler.transform(data[['Age']])
data.head()
scaler = MinMaxScaler()
scaler.fit(data[['Income']])
data['Income'] = scaler.transform(data[['Income']])
scaler.fit(data[['Age']])
data['Age'] = scaler.transform(data[['Age']])
data.head()
Output :
Again Run K-Means Algorithm on Age and Income which is now normalized, the Computed cluster as per our criteria where we told our algorithm to identify 3 clusters
#cluster 1 = 0
#cluster 2 = 1
#cluster 3 = 2
#cluster 2 = 1
#cluster 3 = 2
km = KMeans(n_clusters=3)
y_predicted = km.fit_predict(data[['Age','Income']])
y_predicted
y_predicted = km.fit_predict(data[['Age','Income']])
y_predicted
Output :
array([1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2])
Dropping the Cluster column because it was not normalized, and adding a new column cluster where the data points are normalized.
data['cluster'] = y_predicted
data.drop('Cluster',axis=1,inplace=True)
data.head()
data.drop('Cluster',axis=1,inplace=True)
data.head()
Output :
Now as we have normalized our data, created a new column of it now let's plot the graph and see what are the changes we can see
df1 = data[data.cluster == 0]
df2 = data[data.cluster == 1]
df3 = data[data.cluster == 2]
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.xlabel('Age')
plt.ylabel('Income')
df2 = data[data.cluster == 1]
df3 = data[data.cluster == 2]
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.xlabel('Age')
plt.ylabel('Income')
Output :
Now as we can clearly see that our Red, Green, Blue clusters are perfectly arranged. Now we are ready to find the centroids. To do that we have an amazing function named "cluster_centers_" which is very easy to implement.
# Centroids
# (Contains (X,Y) co-ordinates)
km.cluster_centers_
Output :
array([[0.72268908, 0.8974359 ],
[0.1372549 , 0.11633428],
[0.85294118, 0.2022792 ]])
As we successfully find out all the centroids with there respective co-ordinates let's plot them. In this "[:,0]" is our First Column, and "[:,1]" is our Second Column & "s" is our Marker size.
df1 = data[data.cluster == 0]
df2 = data[data.cluster == 1]
df3 = data[data.cluster == 2]
plt.figure(figsize=(10,8))
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],color="black",marker="*",label="centroid",s=300)
plt.xlabel('Age')
plt.ylabel('Income')
plt.legend()
df2 = data[data.cluster == 1]
df3 = data[data.cluster == 2]
plt.figure(figsize=(10,8))
plt.scatter(df1.Age,df1['Income'],color='red')
plt.scatter(df2.Age,df2['Income'],color='green')
plt.scatter(df3.Age,df3['Income'],color='blue')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],color="black",marker="*",label="centroid",s=300)
plt.xlabel('Age')
plt.ylabel('Income')
plt.legend()
Output :
As you can see that "*" this are the center of our clusters. Now it's time to find out our elbow plot method. Basically, this example which we are currently solving is easy but when you will face some wide data set which has 40-50 features it will become messy and hard to understand. So at this point our Elbow plot used to help us. As we saw in theory we go through the number of "K" like we go from 1 to 10 then we try to calculate SSE which is Sum of Square Error and plot them and try to find the Elbow.
# Elbow plot
k_range = range(1,10) # define K-range
SSE = []
for k in k_range:
km = KMeans(n_clusters=k) # Each iteration we will create new model with cluster = K
km.fit(data[['Age','Income']]) # We are trying to fit both of our important features
SSE.append(km.inertia_) # In KMeans there is a parameter called inertia that will give us the SSE & we append that error to our array
SSE
k_range = range(1,10) # define K-range
SSE = []
for k in k_range:
km = KMeans(n_clusters=k) # Each iteration we will create new model with cluster = K
km.fit(data[['Age','Income']]) # We are trying to fit both of our important features
SSE.append(km.inertia_) # In KMeans there is a parameter called inertia that will give us the SSE & we append that error to our array
SSE
Output :
[5.43401151198818,
2.091136388699078,
0.4750783498553096,
0.3625079900797329,
0.2664030124668416,
0.22020960864009398,
0.17299621932455464,
0.13265419827245162,
0.10383752586603559]
# Plotting our Elbow Graph
plt.xlabel('K')
plt.ylabel('Sum of Square Error')
plt.plot(k_range,SSE)
plt.ylabel('Sum of Square Error')
plt.plot(k_range,SSE)
Output :
So as you can see in the about graph that the value of our "K" is 3 and we made quite a good prediction I'll say but in the complex dataset, it's kinda complicated.
Hey, guy's did you liked our content? Please leave a comment below and give us any suggestions you want and don't forget to share this content with your friends.








































No comments:
No Spamming and No Offensive Language