14 MOST ESSENTIAL Concepts About Decision Tree You Need To Know Right Now [BE A PRO]

TREE

Decision Tree is a classification algorithm which comes under the Supervised Learning Technique.

In this revolutionizing world of Machine Learning we had covered various topics such as:

and many more interesting topics in a very simple way with minimum use of complex mathematics. We had also included multiple examples of codes for a better understanding of there implementation.

So our today’s topics is Decision Tree. A topic that every Machine Learning enthusiastic is awarded about.

Before directly diving into Decision Tree. Let us see, what all things that we are going to accomplish in this blog.

(1) What is a Tree?

(2) CART(Classification And Regression Tree)

(3) What is Classification?

(4) Why we need to Classify?

(5) What is Decision Tree?

(6) Important Terminologies of a Decision Tree

(7) What is Entropy?

(8) How does Decision Tree work?

(9) What is the Gini Index?

(10) What is Information Gain?

(11) Application of Decision Tree

(12) Advantages of Decision Tree

(13) Disadvantages of Decision Tree

(14) Decision Tree Example

I hope The agenda of today's session is absolutely clear to you all.

Now Let’s dive in.

(1) What is a Tree?

- In linear the data structure, data is organized in sequential order, and in the non-linear data structure, data is organized in random order.

- The tree is a very popular data structure used in a wide range of applications. A Tree data structure can be defined as follows.

- A tree is a non-linear data structure that organizes data in a hierarchical structure.

- The tree represents the nodes connected by edges.

GLOSSARY TREE

Root:

-In a Tree data structure, the first node is called the Root Node. Every Tree must have a root node.

-Root node is the origin of tree data structure. In any tree, there must be only one root node. We never have multiple root nodes in a Tree.

Parent:

- In a Tree type data structure, the node which is a predecessor of any node is called as Parent Node.

- Parent Node can also be defined as “The Node Which Has Child/Children's”.

-The Root Node is the only node that does not have a Parent Node.

Child:

- The immediate successor of a node is called as Child Node.

- In a Tree, any parent node can have any number of Child Nods.

Siblings:

- Children of the same Parent is called as Siblings. In simple words, the nodes with the same parent are called sibling nodes.

Subtree:

- A Subtree is a set of nodes and edges comprised of a parent and all the descendants of that parent.

Leaf Node:

- The nodes which do not have any child is called Leaf Node.

- Leaf Nodes are called terminal nodes.

(2) CART( Classification And Regression Tree)

So let us see the 2 different categories where Decision Trees can be used.

CART

(i) Classification

(ii) Regression

(i) Classification:

- Classification where all the output is categorical i.e either they are True or False, Male or Female etc or the output belongs to certain category i.e did you scored A, B, C or D grade in your final examination etc.

- In Classification, a Classification Tree will determine a set of logical if-then conditions to classify problems.

Example : Identifying the fruit is an Apple or Orange.

CLASSIFICATION TREE

(ii) Regression:

- Here we predict the output value as a specific number.

- In Regression, a Regression Tree is used when the target variable is numerical or continuous in nature.

- We fit a regression model to target variables using each of the independent variables.

- Each split is made based on the sum of the square error.

REGRESSION TREE

For today’s topic we are going to only focus on the Classification Trees.

(3) What is Classification?

- Classification is a process of categorizing a given set of data into classes, It can be the performance on both structured or unstructured data.

- The process started with predicting the class of given data points.

- The classes are often referred to as target, label, or categories.

E-MAIL IS SPAM OR HAM

Classification is a technique of categorizing the observation into different category.

Basically we are doing is, we are taking data analyzing it, and on the basis of some of the conditions we are dividing it into various categories.

(4) Why do we classify?

- We classify it to perform predictive analysis on it.

For Example :

When we receive an E-mail, the machine predicts it either it could be a spam or not spam. On the bases of that prediction we add that particular mail to the respected folder.

In general our Classification algorithm handles questions like:

a.) Is this data belong to A, B, or C.

b.) It is a Spam or a Ham.

c.) Is that person is a Male or a Female?

(5) What is Decision Tree?

A Decision Tree is a graphical representation of all the possible solutions to a decision based on certain conditions.

We can also say that the decision tree is a flowchart or a tree shape diagram which always starts with a Root Node. Each branch of the tree represents a possible decision, occurrence, or reaction.

Decisions made can be easily explained.

Let’s see an example where you want to purchase a house.

DECISION TREE FOR PURCHASING HOUSE

In this example of the Decision Tree, we want to buy a but at certain conditions. Such as the price of the house should be ₹.5000000 if it's in Mumbai than buy it or else don't buy it and if it's in Pune check if it has 2 BHK or not if it's 2 BHK then purchase the house or else don't purchase the house.

(6) Important Terminologies of a Decision Tree

Basically there are 6 main terminologies regarding Decision Tree.

(a) Entropy

(b) Pruning

(c) Gini Index

(d) Information Gain

(e) Reduction in Variance

(f) Chi-Square

(a) Entropy:

Entropy is the measure of Randomness or Unpredictability in the Dataset.

FRUIT BASKET

If I tell you to pick you the fruit from the basket with your eyes close then the entropy will be max. But in real life entropy should be minimum.

(b) Pruning:

Basically we can say that this is the opposite of Splitting, in this we remove unwanted branches from the tree.

For Example :

PRUNING

We removed the unwanted branch from the tree because we don’t want it.

(c) Gini Index :

The measure of impurity (or purity) used in building Decision Tree in CART is Gini Index.

(d) Information Gain :

The information Gain is the decrease in entropy after a dataset is split on the basis of an attribute. Constructing a decision tree is all about a fighting attribute that returns the highest information gain.

Information Gain = Entropy(s) – [ (Weighted Average) * Entropy(each feature)]

(e) Reduction in Variance :

Reduction invariance is an algorithm used for continuous target variable (regression problems). This split with lower variance is selected as the criteria to split the population.

(f) Chi-square :

It is an algorithm to find out the statistical significance between the difference between sub-nodes and parent node.

Now the main question is how will you decide the best attribute? For now just understand that you need to calculate something called Information Gain.

The attribute with the highest information gain is considered as best. Before understanding information gain let’s first understand entropy.

(7) What is Entropy?

Entropy is the metric, which measures the impurity of something or in other words you can say that it is a first step to do before you solve the problem for Decision Tree.

Let’s understand a term known as Impurity before understanding Entropy.

LOW / HIGH ENTROPY

For Example :

Let’s say you have a dataset and you are trying to distinguish between various fruits and instead of taking multiple factors under consideration, you only took color as the only feature for differencing the fruits.

So what will happen is, for example there are green apple and red apple and strawberry in the dataset. You will keep the red apples and the strawberry in one basket. So here we can say that in this impurity is not zero which means that the impurity in this exists.

ENTROPY

Now come back to the word Entropy.

* Defines randomness in the data.

* Entropy is just a metric that measures the impurity.

* It is the first step to solve the problem of a decision tree.

ENTROPY GRAPH

From the above graph you can see that if the probability is 0 or 1 then it means that they are highly impure and if the value is 0.5 then it means that the value is very pure.

Now you will be thinking why the value of the entropy is pure at 0.5? Let me derive it mathematically.

As you can see that the formula of entropy is :

Entropy(s) = -P(yes) log2 P(yes) – P(no) log2 P(no)

Where;

* s is the total sample space.

* P(yes) is the probability of Yes.

* P(no) is the probability of No.

If number of yes = number of no i.e P(s) = 0.5

→ Entropy(s) = 1

If it contains all yes or all no i.e P(s) = 1 or 0

→ Entropy(s) = 0

Let’s start with conditions :

1.) Condition 1 Probability = 0.5

E(s) = -P(yes) log2 P(yes)

When P(yes) = P(no) = 0.5 i.e YES + NO = Total Sample(s)

E(s) = 0.5

Now substitute that value 0.5 into the formula.

E(s) = 0.5 log2 0.5 – 0.5 log2 0.5

E(s) = 0.5(log2 0.5 – log2 0.5)

E(s) = 1

2.) Condition 2 Either we have total YES or total NO

(i) Total YES :

E(s) = -P(yes) log2 P(yes)

When P(yes) = 1 i.e YES = Total Sample(s)

E(s) = 1 log2 1 … log 1 = 0

E(s) = 0

(ii)Total NO :

E(s) = -P(no) log2 P(no)

When P(no) = 1 i.e YES = Total Sample(s)

E(s) = 1 log2 1 … log 1 = 0

E(s) = 0

(8) How does Decision Tree work?

I am sure most of you have a general idea about how a decision tree works, but for better understanding and for clear knowledge let’s take an example dataset and understand it diagrammatically.

DATASET

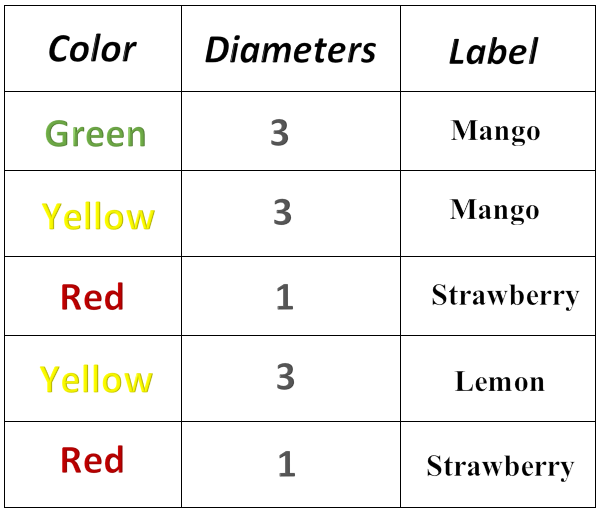
In this dataset each row is an example and the initial 2 columns provide features or attributes that describe the data and the last column gives the label or the class we want to predict.

Now if you look at this dataset this is very straight forward except from 1 thing. If you look at our 4^th label column and compare that with 1^st and 2^nd labels you will notice that the features are the same but the label is different.

Let’s see diagrammatically how the decision tree handles this case.

In order to build this decision tree we will be using CART which we have discussed above.

Step1:

We will start with the root node as a tree and all the nodes receive a list of rows as input and root will receive the entire training dataset.

Step2:

Now each node will ask True or False questions about one feature and in response to that question we will split or partition the dataset into 2 different subsets these subsets then become an input to 2 child nodes. The goal of the question is to finally unmix the label as we proceed down or in other words to produce the purest possible distribution of the labels at each node.

SPLITTING

Step3:

The input of this node contains only one single type of label so we could say that it’s perfectly unmixed there is no uncertainty about the type of label as it consists of the only strawberry. On the other hand labels in this node are still mixed up. So we will ask another question to further drill it down. But before that, we need to understand which question to ask and when to do that we need to quantify how much question helps to unmix the label and then we can quantify the amount of uncertainty at a single node using a metric called Gini impurity and we can quantify how much a question reduces that uncertainty using a concept called Information Gain. We will use this to ask the best questions at each point and then we will iterate the steps and we will recursively build a tree on each of the new nodes.

FURTHER SPLITTING

Step4:

We will continue to divide the data until there are no further questions to ask and then we will finally reach our leaf.

FOUND LEAF NODE

(9) What is the Gini Index?

Gini index means that, if we select 2 items from a given dataset at random then they must be of same probability and class for this population should be pure.

It works with the categorical target variable “True” or “False”.

1. It performs only Binary (0/1) splits

2. Higher the value of Gini index is higher the homogeneity.

3. CART (Classification and Regression Tree) uses the Gini method to create binary splits.

Steps to Calculate Gini for a split :

1. Calculate Gini for sub-nodes, using formula sum of the square of probability for True and False (p²+q²).

2. Calculate the Gini index for split using the weighted Gini score of each node of that split.

(10) What is Information Gain?

In Information Gain, Less impure node requires less information to describe it and a more impure node requires more information to describe it. Information theory is a measure to define this degree of disorganization in a system known as Entropy. If the sample is completely homogeneous, then the entropy is 0 and if the sample is equally divided into half at each side i.e 50% - 50% then it has an entropy of 1.

Entropy can be calculated using the formula:

Entropy = -p log₂ p — q log₂q

Here p is the probability of success and q is the probability of failure in that node. Entropy is also used with a categorical target variable. It chooses the split which has the lowest entropy compared to the parent node and other splits. The lesser the entropy, the better it is.

Steps to calculate the entropy for a split:

Step 1: Calculate entropy of parent node.

Step 2: Calculate entropy of each individual node of split and calculate the weighted average of all sub-nodes available in the split.

We can derive information gain from entropy as 1- Entropy.

(11) Application of Decision Tree

We use Decision Tree more often then you think. Here are some of the real world application of Decision Tree which will blow you mind.

(i) Telecommunication Industry :

TELECOMMUNICATION

Telecommunication Industry uses this very often as if you want to chat with customer care, you might have noticed that they guide you, by instructing you to provide you the best services they can. For example Press 1 for Hindi, Press 2 for English so on.

(ii) Online Shopping:

ONLINE SHOPPING

Online The marketing industry uses the Decision Tree for several purposes, such as based on the last purchase or based on the last search of the product they show you more similar products. Amazon uses this very often, we search for sports shoes it will show us all kinds of sports shoes.

(iii) Handle our Craving :

PIZZA

I know this is funny, but give it a thought. Let’s say you have 20$ and we are very hungry. So what will you do? eat 1 pizza or eat 2 burgers. I leave this completely up to use guys😂.

(12) Advantages of Decision Tree :

Let us see the Advantages of Decision Trees :

* It is simple to understand.

* It is not difficult to interpret and visualize it.

* Very Less efforts are required for data preparation.

* We can handle both numerical and categorical data with the help of the Decision Tree.

* Performance of the Decision Tree is not Effected by the non-linear parameters.

(13) Disadvantages of Decision Tree :

Let us see the Disadvantages of Decision Trees :

* The Primary disadvantages of the decision tree are overfitting. Overfitting occurs when the algorithm capture noise in the data.

* In decision tree there is also a problem of high variance. The model can get unstable due to small variance in the data.

* In a decision tree is there is Low Biased tree. A highly complicated decision tree tends to have a low bias which makes it difficult for the model to work with new data.

* Calculation can get very complex particularly if many values are uncertain and if many outcomes are linked.

(14) Decision Tree Example :

Will that movie will win Oscar or Not?

CSV File : Classification_dataset

# Import all libraries

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# Import Dataset

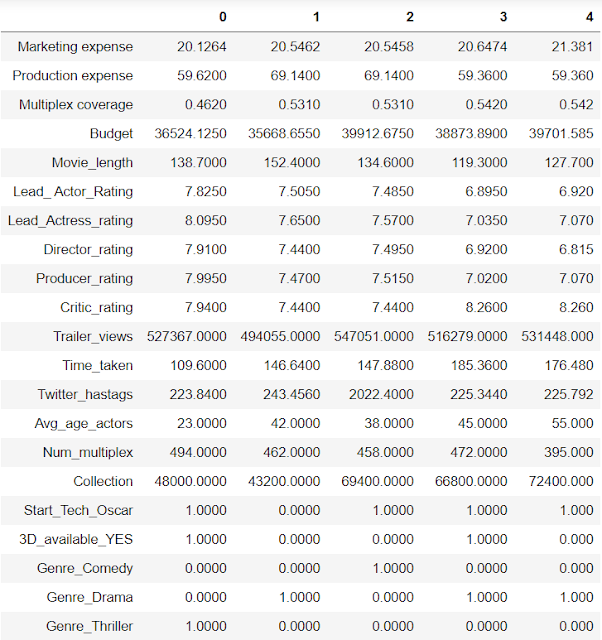
df = pd.read_csv("E:\college_pics\Rainbow6\classification.csv",header=0)

df.head().T

Output :

# Display information of the dataset

df.info()

Output :

# Handel Missing Values

df['Time_taken'].fillna(value = df['Time_taken'].mean(),inplace=True)
df.head().T

Output :

df.info()

Output :

# Creating Dummy Variables

df = pd.get_dummies(df,columns = ['3D_available','Genre'], drop_first=True)
df.head().T

Output :

# X and y split

X = df.drop('Start_Tech_Oscar',axis=1)
type(X)

Output :

pandas.core.frame.DataFrame

X.shape

Output :

(506, 20)

y = df['Start_Tech_Oscar']
type(y)

Output :

pandas.core.series.Series

y.shape

Output :

(506,)

# Train-Test Split

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=0)

X_train.shape

Output :

(404, 20)

X_test.shape

Output :

(102, 20)

# Training Classification Tree

from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(max_depth=3)
model.fit(X_train,y_train)

Output :

DecisionTreeClassifier
(class_weight=None, criterion='gini', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')

# Predicting Values using the trained model

y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
y_train_pred.shape

Output :

(404,)

y_test_pred

Output :

array([0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1,
0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0], dtype=int64)

# Model Performance

from sklearn.metrics import accuracy_score, confusion_matrix

confusion_matrix(y_train, y_train_pred)

Output :

array([[172, 14],
[126, 92]], dtype=int64)

confusion_matrix(y_test, y_test_pred)

Output :

array([[39, 5],
[41, 17]], dtype=int64)

accuracy_score(y_test, y_test_pred)

Output :

0.5490196078431373

dot_data = tree.export_graphviz(model, out_file=None, feature_names=X_train.columns, filled=True)

from IPython.display import Image
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())

Output :

model2 = DecisionTreeClassifier(min_samples_leaf=20, max_depth=4)
model2.fit(X_train,y_train)

dot_data_2 = tree.export_graphviz(model2, out_file=None, feature_names=X_train.columns, filled=True)
from IPython.display import Image
import pydotplus
graph2 = pydotplus.graph_from_dot_data(dot_data_2)
Image(graph2.create_png())

Output :

accuracy_score(y_test, model2.predict(X_test))

Output :

0.5588235294117647

* Decision Tree Summary:

Let us summarize everything:

- We saw what is Tree and some important terms related to it.

- CART: Classification and Regression Tree.

- Then we saw what classification is and a SPAM and HAM image.

- After that, we saw why do we classify?

- We understood the Decision Tree with a House Purchasing example.

- Some Important Terminologies.

- Then we saw what is Entropy. In which we saw a diagram and a graph with values 0, 0.5, and 1.

- Then we saw how the Decision Tree works with an example.

- We also saw the Gini index and steps to calculate it.

- Which lead us to Information Gain and how to calculate it.

- Then we saw the various real-life application of Decision Tree.

- After that, we had a glimpse of the Advantages of the Decision Tree.

- Everything has its own disadvantages, So we also saw Disadvantages of the Decision Tree.

- Then we saw a coding step by step example of the Decision Tree.

Did I Miss Anything?

Now I'd like to hear from you:

- Which Concept did you like the most?

- What else would you like us to cover on this topic?

- What are the 5 most informative concepts you found in this blog?

Do comment, your answers and don't forget to share it with your friend so, you can discuss more this topic.

InfinityCodeX