Google Stock Price Prediction Using RNN - LSTM Python

Google Stock Price Prediction Using RNN - LSTM Python

In this article, we are going to look at an outstanding end-to-end real-life Recurrent Neural Network (RNN) - LSTM project where we will predict the price of google stock. We will be using Python, Keras, Jupyter Notebook, and Tensorflow for this project.

Before directly diving into the code let’s have an overview of the topics such as RNN and LSTM network.

                                                  

STOCKS IMAGE

Q.)What is RNN?

RNN also is known as Recurrent Neural Network has unique properties that allow them to be more effective for sequence data, sequence data can be a variety of data sources it can be anything from timestamps sales data or sequence of text in a sentence or biological data like heartbeat data overtime etc.

Basically, RNN helps us to predict future sequential data more accurately which learns from history.

To do this properly, we need to somehow let the neuron “Know ” about its previous history of outputs. One of the easy ways to do this is to simply feed it’s output back into itself as an input.

Let’s look at the normal neuron in feed-forward network

                                 

NEURON

                              

Now how we will take advantage of being able to relay back the history with a neuron?

                                   

NEURON INVERSE

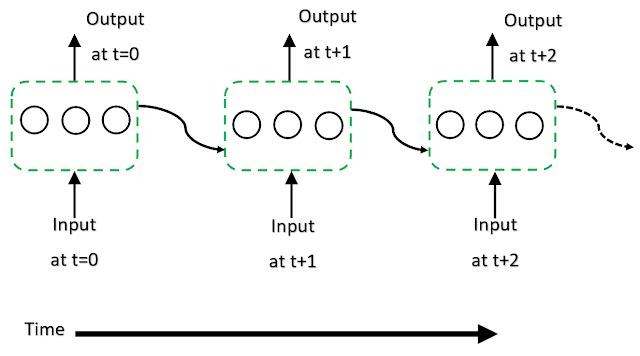
Here we can use a Recurrent Neuron. In Recurrent Neuron the main difference here not only sends the output out to the next layer, it takes that output and feeds it back to itself. So over time, we can unroll this.

Now go one timestamp into the past at Time(t-1) so as you can see we have some input coming in at t-1 this can be batch of sequence data which are aggregated and passed to the activation function and we get the output of this Recurrent a neuron at t-1.

                                           

FUTURE NEURON

As time goes on we end up doing for that next input batch of another sequence or input at time t, here we are not only going to feed in the input at time t but we also feed in the information of the output of Recurrent neuron times (t-1) which then give us the output at time t. Then we take that output at time t and feed it along with the input at a time (t+1) that way we are retaining the historical information. This is the Recurrent neuron essentially unrolled throughout time.

                                             

RECURRENT NEURON

Cells that are a function of inputs from previous time steps are known as memory cells.

RNN is also flexible in their inputs and outputs, for both sequence and single vector values.

We can actually, create entire layers of Recurrent Neurons.

Here is an simple diagrammatic representation of it.

(Artificial Neural Network) ANN :

                                                    

NORMAL ANN

(Recurrent Neural Network) RNN :

                                               

NORMAL RNN

Now we can just unroll this layer in the same fashion. We pass input as time t = 0 into the layer and then the output of the layer is time t+1, than t+2, and so on.

                                                   

RNN UNROLLED LAYER

As I have mentioned earlier that the RNN are very flexible in their inputs and outputs. There are different types of architectures we can use here. Let’s see some of them:

1.) Sequence to Sequence (Many to Many):

                                          

SEQUENCE TO SEQUENCE

In this, you pass in a sequence and you expect a sequence out.

For Example : We have an input of 5 words now you have to predict the output of  5 words.

2.) Sequence to Vector (Many to One):

                                               

SEQUENCE TO VECTOR

In this, you pass in a sequence and you expect a vector as an out.

For Example : We have an input of 5 words now you have to predict the output of the next  1 words.

3.) Vector to Sequence (One to Many):

                                              

VECTOR TO SEQUENCE

In this you pass in a vector i.e a single value and you expect a sequence as an out.

For Example : We have the input of 1 word now you have to predict the output of the next  5 words.

A basic RNN has a major disadvantage, we only really “remember” the previous output. If we think back that unrolled diagram we were only feeding in the of 1 timestamp into the past and what happens is if we have really long histories we begin to start to forget the older historical samples since we are only really looking at the out of the last previous t-1 and it will be really great if we could keep the track of long history and not just that short term memory. Another issue that arises during training is the “vanishing gradient”.

Before directly diving into the LSTM (Long Short Term Memory Units). We will have an overview of Vanishing Gradient.

Let’s discuss the 2 main issues i.e Exploding & Vanishing Gradients.

As our networks grow deeper and more complex, we have 2 issues arises:

-Exploding Gradients

-Vanishing Gradients

Recall that the gradient is used in our calculation to adjust weights and biases in our network, if you don’t have any idea about Gradient you may check our GradientDescent article.

This errors might arise during backpropagation :

                                                

NEURAL NETWORK

Now for complex data we such as complex image data or complex sequence data we end up needing deeper networks i.e we need more hidden layers in order to actually learn the patterns that are in our data.

Now what happens is there’s this vanishing or exploding gradient issue that arises during the backpropagation step. So recall we are going to calculate some sort of loss metrics on the output layer and then backpropagation error all the way back to the input layer and if we have a lot’s of hidden layers then we’re having the update to the weights and biases be a function of many other derivatives that we’re calculating along the way back.

- So backpropagation goes backward from the output to the input layer, propagating the error gradient.

- For deeper networks issues can arrive from backpropagation, vanishing and exploding gradients.

                                                      

BACK PROPAGATION

- As you go back to the “lower” layers closer to the input layer, gradients often get smaller, to a vanishing gradient is usually the more common problem although they can technically explode on the way back. But as you are going back and back closer to those input layers there are gradients are getting smaller and eventually what happens is they’re so small by the time it gets to the input layer that the weights never really change that much at those lower input levels.

- That’s actually, a big problem because we want to be able to detect larger basic patterns in our data right out close to the input layer and have the deeper layers focus on the smaller details or in smaller details and patterns.

- And yes the opposite can also occur that the gradients explode on the way back, causing issues.

Now let’s discuss why this is actually occurring and how we can fix it and let’s also discuss how these issues specifically affect the RNN and how we can use the LSTM units and get a recurrent unit to also fix this to understand what actually happening let’s take a look at a really common activation function such as sigmoid. Now as we know that the sigmoid activation function squeezes the input to fit between 0 & 1.

                                                 

SIGMOID

However let’s take a closer look at what happens when your inputs start to get further away from zero.

                                                         

SIGMOID

The further away your input is from zero. The rate of change in the sigmoid function is actually decreasing rapidly and that rate of change that is the derivatives of the sigmoid functions and we already know that the backpropagation and the gradient calculation is essentially just calculating that derivative in multiple dimensions as you go back through into the hidden layers.

* When N hidden layers use an activation like the sigmoid function, N small derivatives are multiplied together.

* The gradient could decrease exponentially as we propagate down to the initial layers.

* We can use other activation function such as ReLU which doesn't actually saturate those larger positive values.

* The main benefit of using ReLU here is that doesn't matter how large your input value is going to be beyond 0. You are not going to exponentially decrease the rate of change.

The other a possible solution is the Batch Normalization where your model will normalize each batch using that particular batches mean and standard deviation, and that has also been founded to alleviate the issue of vanishing gradient descent.

So apart from things such as Batch Normalization, researchers have also used “Gradient Clipping”, where gradients are cut off before reaching a predetermined limit (eg: Cutt off gradients to be between -1 and 1).

RNN for Time Series presents their own Gradient Challenges, let’s explore special LSTM (Long Short Term Memory) neuron units that help fix these issues!

*LSTM ( Long Short Term Memory ):

Many of the solutions previously presented for the vanishing gradients can also apply to

RNN: different activation functions (ReLU), batch normalizations, etc…

However because of the length of time series input, these could slow down the training.

A possible solution would be to just shorten the time steps used to prediction, but this makes the model worse at predicting longer trends. So maybe looking back 20 time steps for the 21^st prediction you just look back 5-time steps to get the next prediction. However, this makes the model worse at predicting longer trends. So we still want to able to use a long time sequence in order to predict the next item in the sequence.

Another issue RNN faces are that after awhile the network will begin to “forget” the first inputs, as information is lost at each step going through the RNN.

We need some sort of “long-term memory” for our networks. So this is where LSTM (Long Short Term Memory) cell was created to help address these RNN issues.

Let’s see the working of an LSTM cell:                                                   

RNN CELL

Take a look at what a single Recurrent neuron would actually be doing is essentially it’s taking in both the previous output and then the current input and then producing the next output.

                                                                         

RNN CELL LABELED

instead of saying it output or input, we will refer to these as hidden state and then our current feature X going in. So basically we have Ht-1 going along with X of T and that produces Ht. So in a standard RNN essentially what we do is we just have a single hyperbolic tangent function and then what we are doing, we are combining Ht-1 with Ht multiply that with some weight matrix then adding a bias to it and then passing it through the hyperbolic tangent function and that gives us back our Ht.

                                                                  

RNN CELL LABELED FORMULA

And we just repeat that through the next recurrent neuron or an extra current layer.

So LSTM also have this chain-like structure. But a repeating module have slite difference to it and instead of just having a single NN layer. There would be actually going to be 4 layers working and interacting in a special way and the way we end up getting 4 is the fact that not only will we keep track of just a single historical memory with Ht-1 we’re keeping track of both long term memory input and the short term memory input and that creating a new long term memory output and then use short term memory output along with the current input at time t and then we produce the output with time t.                                                 

STEPS OF LSTM :

Before diving into the steps let’s see some of the notation we’re going to be using so essentially.

So essentially we are going to have 4 main components inside the LSTM.

                                                      

LSTM 4 MAIN COMPONENTS

We have: Forget Gate, Output Gate, Update Gate, and an Input Gate.

*Forget Gate: As the name suggests, Forget Gate will decide what to forget from the previous memory units.

*Input Gate: As the name suggests, Input Gate will decide what actually accept into the neuron.

*Update Gate: As the name suggests, Update Gate will update the memories.

*Output Gate: As the the the name suggests, Output Gate will actually output the new long term memory.

                                                

SIGMOID CELL

A Gate optionally lets some information through and essentially we can just think of this as mathematically it’s a sigmoid function. It’s either going to end up a sequence between a 0 or 1 and if it’s 0 we don’t let that information go and if it’s a 1 we let it go.

                                                      

GENERAL STRUCTURE OF LSTM

So here is the general structure of LSTM and we are accepting both Long Term and Short Term memory, we can think of this as going to be passed in through conveyor belts inside of this neuron and what we end up happening are it just ends up kind of running down straight the enitre chain and has some kind of linear interactions with a few functions inside of the cell.

Now for the purpose of a mathematical notation we’re gonna relabel some of these and we’re going to label them as such.

                                                  

GENERAL STRUCTURE WITH NOTATION

So what are the actual linear interactions and functions going on inside of LSTM? Well, here we can see the entire LSTM cell.

Now let’s go through the process step by step :

1.] The 1^st step of LSTM is to decide what information is going to throw away from the cell state essentially what we are going to forget? So we end up creating is a forget gate layer or ft.

                                                 

INSIDE OF LSTM

So we end up creating is a forget gate layer of ft. Remember those gates are essentially just passing things through a sigmoid function where the closer it is to 0 that means fewer weights we are giving it. The closer it is to 1 the more weights we are giving it. So in the context of the forget gate layer the closer it is to 0 means forget about it and get rid of it and if it closer to 1 than remember this it's important. So this is what ft is doing. Notice that it's essentially a linear combination of ht-1 that previously hidden state combines with the input Xt. Then we have our own sets of weights for this forget gate layer plus bias and then we pass it through an activation function and then we get ft then the next step after this is to decide what new information are we going to store into the cell state?

2.] In the 2^nd step we have to decide what new information we are going to store into the cell state. This has 2 parts to it :

                                                    

INSIDE OF LSTM STEP 2

(i) We have a sigmoid layer that we’re going to label the input gate layer which is essentially going to decide what values are we going to update.

(ii) We have a hyperbolic tangent layer that creates a vector of new candidate values which will say Ct but we will label this with a tilde on top of it. These are the new candidate values that will eventually helpful in some sort of weighing be updating the cell state. So we have that input gate layer deciding which value we’re going to update in the hyperbolic tangent layer which is creating a vector of those new candidate values.

3.] Now it’s time to update the old cell state which is Ct-1. In order to calculate the new cell state Ct that we’re going to end up outputting.

                                                    

INSIDE OF LSTM STEP 3

So what we are doing is that we multiply the old state by ft forgetting the things that we decided weren’t that important due to the forget gate layer. Then we add it times the new candidate values. So essentially these are the new candidate values for the cell state scaled by how much we decided to update each state value.

4.] Finally we have to decide what we are going to output? So this output will be based on our cell state. That actually a filtered version. First, we will end up doing is we run a sigmoid so that top equation which decides what parts of the cell state we are going to output. Then we put that cell state through the hyperbolic tangent function and what the hyperbolic tangent does is it pushes all the values to be between -1 and 1 and then we’re gonna multiply it by the output of that initial sigmoid gate of Ot so that we only output the parts of that we decided to.

                                                  

INSIDE OF LSTM STEP 4

Before directly diving into the coding first, get the data :

Google_Data

This data set contains:-

1.) Data: Stock information date. 

2.) Open: Opening on a particular date.

3.) High: Highest price on that data.

4.) Low: Lowest price on that date.

5.) Close: Stock pricing closed that date.

6.) Adj Close: Adjusted close price.

7.) Volume: Volume of share.

We will be reading this data in chunks of 30 days. So we will be training our neural network on 30 days data we will be predicting the 31st day and then similarity we will again skipping the last data and then again we will be taking from 1 to 31 days and then we will be predicting at 32nd day.

Steps To Build Stock Prediction Model:

i.)    Importing & Preprocessing Data

ii.)   Building The RNN model

iii.)  Predicting Values

iv.)   Checking The Accuracy

i.) Importing & Preprocessing Data:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

data = pd.read_csv(r"E:\New folder\GOOG.csv", date_parser=True)
data.head()

Output:

DATA

# Divide Data into Training and Test set


# Training Data


data_training = data[data['Date']<'2020-05-01'].copy()
data_training

Output:

TRAINING DATA

# Divide Data into Training and Test set


# Test Data


data_test = data[data['Date']>='2020-05-01'].copy()
data_test

Output:

TEST DATA

training_data = data_training.drop(['Date','Adj Close'],axis=1)
training_data.head()

Output:

TRAINING DATA HEAD

Here we have to predict the Open i.e opening price of that particular stock.

# Data Preprocessing


from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()

training_data = scaler.fit_transform(training_data)
training_data

Output:

MIN-MAX SCALER DATA

X_train = []
y_train = []

for i in range(30, training_data.shape[0]):
    X_train.append(training_data[i-30:i])
    y_train.append(training_data[i,0])

X_train, y_train = np.array(X_train), np.array(y_train)

X_train.shape

Output:

(173, 30, 5)

ii.) Build The RNN Model:

# Building LSTM

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout

regression = Sequential()
regression.add(LSTM(units=50, activation="relu", return_sequences=True, input_shape=(X_train.shape[1], 5)))
regression.add(Dropout(0.2))

regression.add(LSTM(units=50, activation="relu", return_sequences=True, input_shape=(X_train.shape[1], 5)))
regression.add(Dropout(0.3))

regression.add(LSTM(units=50, activation="relu", return_sequences=True, input_shape=(X_train.shape[1], 5)))
regression.add(Dropout(0.4))

regression.add(LSTM(units=50, activation="relu"))
regression.add(Dropout(0.5))

regression.add(Dense(units=1))

regression.summary()

Output:

MODEL SUMMARY

# Compile and Fit the model

regression.compile(optimizer='adam', loss="mean_squared_error")
regression.fit(X_train,y_train,epochs=550,batch_size=32)

Output:

COMPILE AND FIT DATA

iii.) Predict Values:

# Prepare test data

data_test.head()

Output:

TEST HEAD

past_30_days = data_training.tail(30)

df = past_30_days.append(data_test, ignore_index=True)
df = df.drop(['Date', 'Adj Close'],axis=1)
df.head()

Output:

FILTERED DATA

inputs = scaler.transform(df)
inputs

Output:

INPUT TRANSFORM DATA

X_test = []
y_test = []

for i in range(30, inputs.shape[0]):
    X_test.append(inputs[i-30:i])
    y_test.append(inputs[i,0])

X_test, y_test = np.array(X_test),np.array(y_test)
X_test.shape, y_test.shape

Output:

((49, 30, 5), (49,))

y_pred = regression.predict(X_test)
y_pred

Output:

PREDICTED DATA

scaler.scale_

Output:

array([2.13419869e-03, 2.17020477e-03, 1.96903103e-03, 2.12734298e-03,2.24300742e-07])

scale = 1/2.13419869e-03
scale

Output:

468.55993525138933

y_pred = y_pred * scale
y_test = y_test * scale

vi.) Visualize The Data and Check Accuracy:

# Visualize the data

plt.figure(figsize=(14,5))
plt.plot(y_test, color="red", label="Real Google Stock Price")
plt.plot(y_pred, color="blue", label="Predict Google Stock Price")
plt.title("Google Stock Price Prediction")
plt.xlabel('Time')
plt.ylabel('Google Stock Price')
plt.legend()
plt.show()

Output:

DATA VISUALIZATION

 So we hope that you enjoyed this project. If you did then please share it with your friends and spread this knowledge.

Follow us at :

Instagram : 

https://www.instagram.com/infinitycode_x/


Facebook :

https://www.facebook.com/InfinitycodeX/


Twitter :

https://twitter.com/InfinityCodeX1